ITensor

High-performance tensor software
inspired by tensor diagrams

Code Examples

Contracting two ITensors

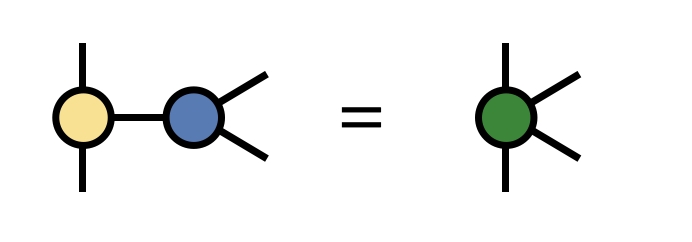
C = A * B

Factoring an ITensor

U,S,V = svd(T,i,j)

To view more code examples, click here.

Installing

The Julia version of ITensor (recommended) is easy to install through the Julia package manager: 

$ julia
julia> ]
pkg> add ITensors



To install other packages such as ITensorMPS, follow the same steps just replacing "ITensors" with the package name.

What Makes ITensor Unique?

Intelligent Indices

The indices of an ITensor have unique identities. When contracting two ITensors, matching indices "find" each other and contract automatically. Adding two ITensors is literally as easy as A+B. Groups of ITensors can be arranged into networks which know their topology.

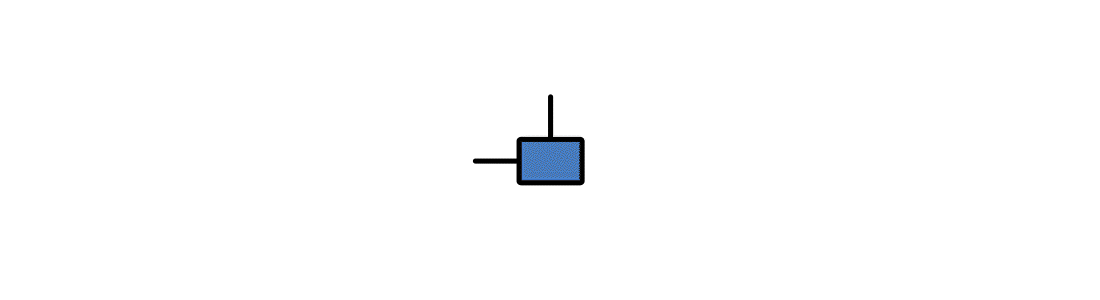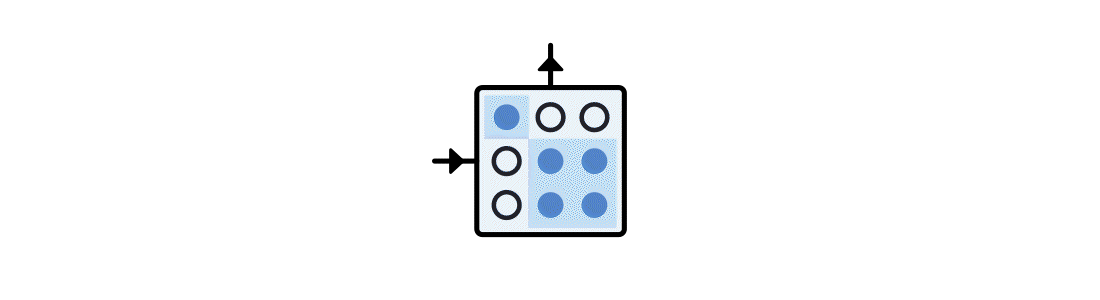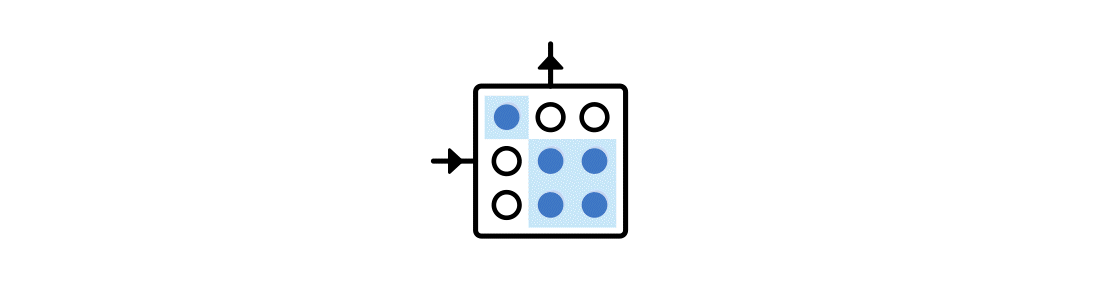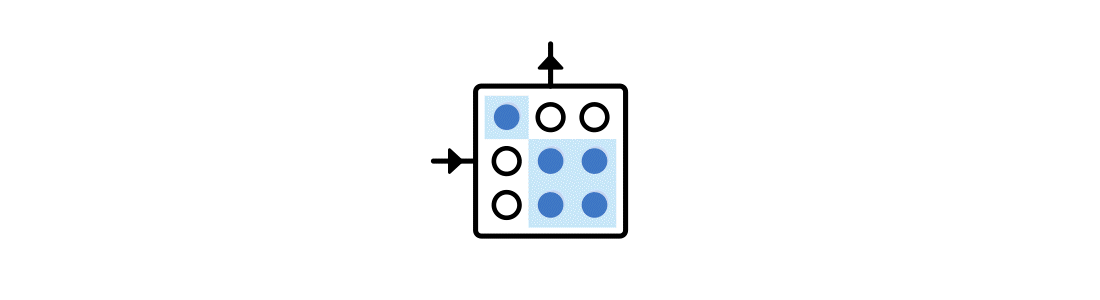
Quantum Number Conserving ITensors

ITensors can be quantum number conserving (invariant under group symmetries) by storing block-sparse data and other information. Quantum number conserving ITensors are nearly as easy to use as regular, dense ITensors.

Quantum Physics Tools

Easily turn human-readable sums of operators into a compressed MPO tensor network, a quantum circuit, and more. These intermediate formats can be used to find ground states, perform real-time or imaginary-time evolution, and other tasks.

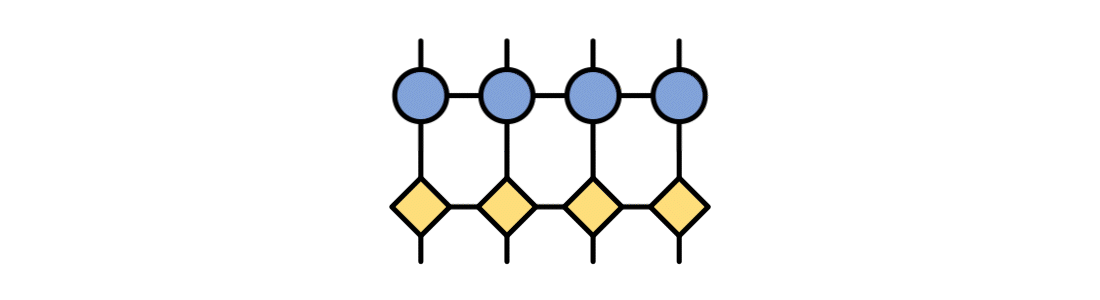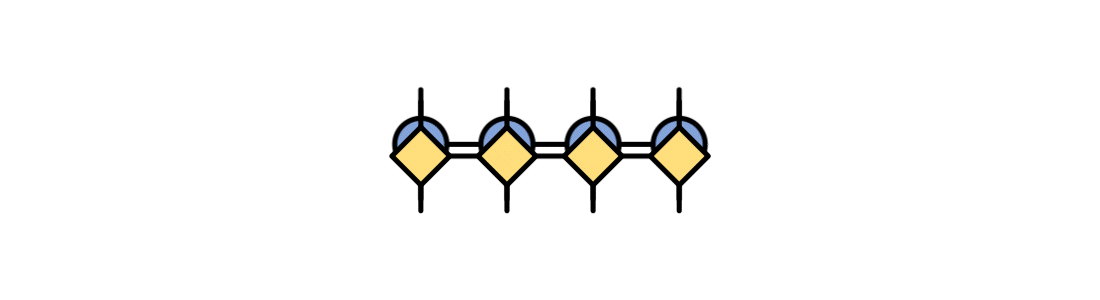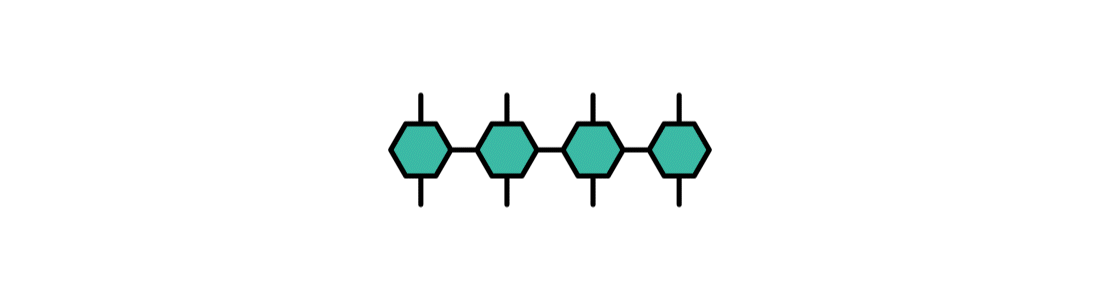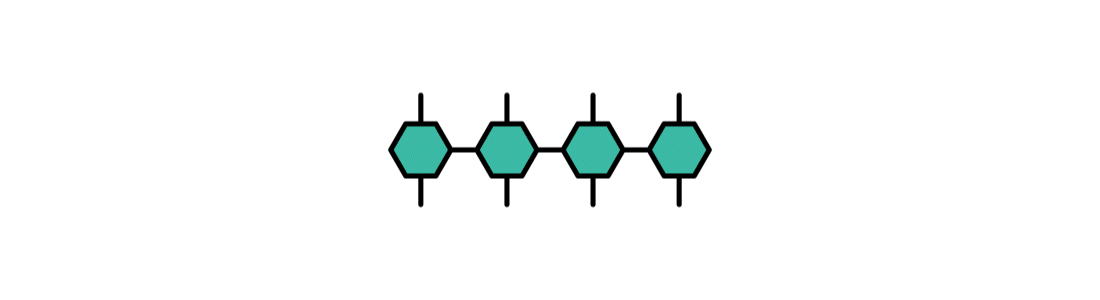
MPS and MPO Algorithms

ITensor includes a full set of algorithms involving matrix product state (MPS) and matrix product operators (MPO), such as state-of-the-art DMRG and time-evolution codes, and algorithms for summing, multiplying, and optimizing MPS and MPOs.